For one reason or another, I was thinking about the checkout process at Trader Joe’s. They often have a checkout process that is different from other stores, where they have customers line up in a single line. When you’re at the front of the line they send you to an available cashier to ring you up. They often have staff at the checkout area to tell you which cashier is open. I haven’t seen such a procedure before going to Trader Joe’s, so I’ll call this procedure the Trader Joe’s checkout. In the traditional way of checking out, which I know you’re familiar with, you go to the back of the line at any cashier you like. Also, all else equal, you typically go to the shortest line. Let’s call this procedure the Traditional checkout.
The question I had was this: Is Trader Joe’s checkout any faster than the traditional checkout, and if so how much faster is it?
I ended up asking the manager at a few Trader Joe’s branches for some information on the number of customers that arrive on an average busy day, and the amount of time a cashier takes to checkout a customer. Using these figures, a model, and a simulator, I was able to come up with an estimate.
And my estimate is… the average waiting time at the Trader Joe’s checkout is 20% shorter than the traditional checkout. Moreover, on average the variance of the Trader Joe’s checkout is 15% lower. The main caveat to these estimates is that I haven’t done a sensitivity analysis for the parameters I used. Also, in my model of the traditional checkout customers don’t change lines while they are waiting.
Now for some plots. Below is the distribution of waiting times for both processes.
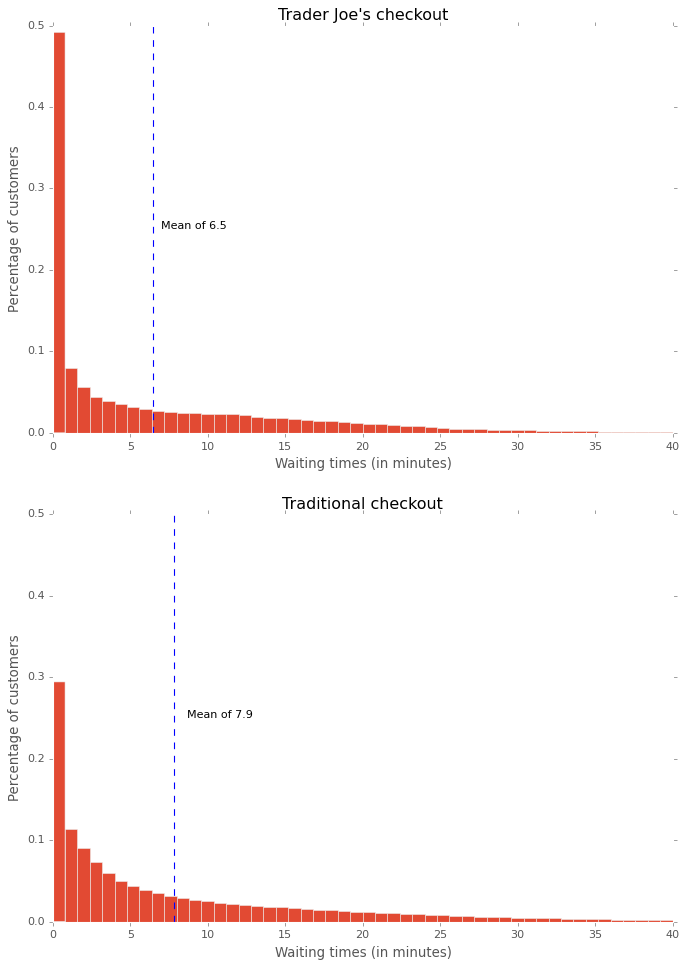
The tail of the waiting time under a traditional checkout system is much longer than the tail under Trader Joe’s checkout system. Also note that there are people who wait in line for 40 minutes before they checkout. This is probably a little unrealistic but it’s easily fixed if I had better estimates of some of the parameters.
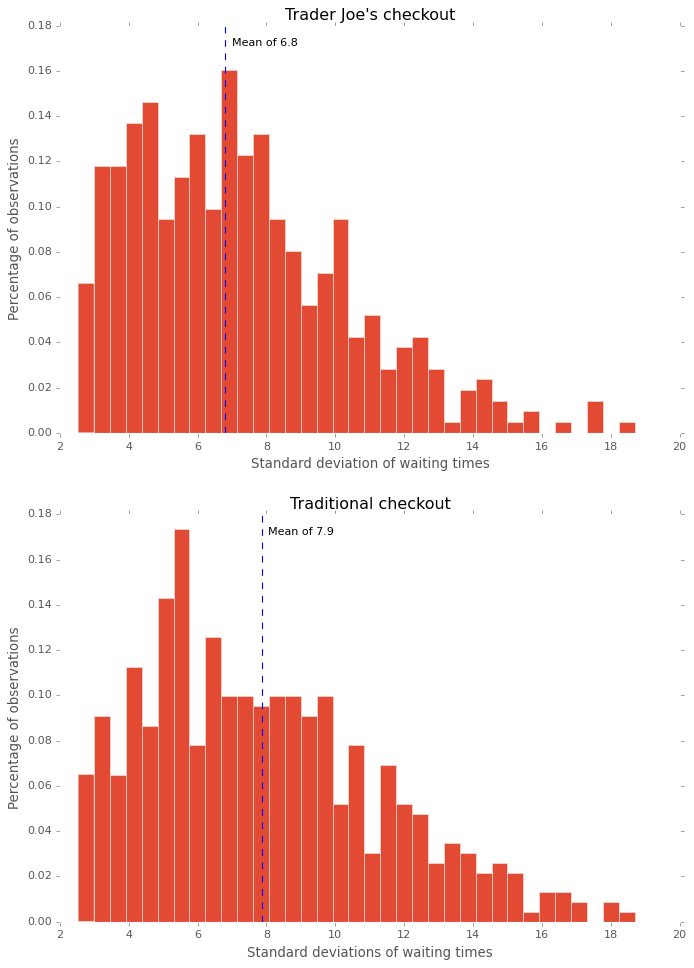
The next plot is the standard deviation for all the customers’ waiting times in a given day. Both systems look similar, but the distribution for the traditional checkout is skewed more to the right.
The rest of this post details exactly how I arrived at this answer. In particular, I detail how I setup the simulations.
Modeling the Checkout
Trader Joe’s checkout
Modeling Trader Joe’s checkout turns out to be very easy:
- Customers randomly decide to checkout, and when they do they enter the checkout line,
- When they are at the front of the line they have to wait for one of the cashiers to finish cashing out their customer,
- When a cashier is free they go to that cashier and they checkout, and
- They leave Trader Joe’s when they’re done checking out.
This process falls neatly into the realm of queueing theory, and the Trader Joe’s checkout is neatly modeled as a multi-server queue.
Traditional checkout
Modeling the Tradition checkout was a little harder. If you are like me you go to the shortest line (or the fastest moving line). This process is greedy, as you make the best decision possible when it’s time to choose a line. Sometimes you choose poorly and you wait longer than you would have under perfect decision making, but you did your best with the information you had. I’m going to assume that once you’ve made this decision you go to that checkout line and stay there. This process can be summed up as:
- Customers randomly decide to checkout,
- They observe all checkout lines and head to the checkout counter with the shortest line,
- They wait in this line until all customers in front of them have checked out before they themselves checkout, and
- They leave Trader Joe’s when they are done.
This process can be modeled as a network of single-server queues. The key here is that the customers behave greedily when routing themselves in the network. This kind of routing is called shortest queue routing.
The arrival and service process
I want to model this as realistically as possible. The queueing framework is a good model for the checkout process, but I’ll need to specify an arrival process and a process for the amount of time it takes for a cashier to ring you up (which I’ll call the service process). Although customers arrive randomly, there is some regularity to their arrival times. This is captured by specifying a distribution for the amount of time between two successive arrivals, called the inter-arrival time. This inter-arrival time should depend on the time of day, since late afternoon’s are probably busier than mornings or evening.
The service process is random as well. We just need to specify a distribution for how much time it takes a cashier to checkout a customer. Unlike the arrival process, the service process does not depend on the time of day. I’ll let $\mu$ denote the rate at which a cashiers checkout customers.
Some data
When I was at Trader Joe’s the other day, I asked the manager about how much traffic he sees on a busy day, and how fast cashiers are on average. He told me that on busy days there are about 2700 customers, and that a cashier will checkout 30-40 customers per hour. I asked the same questions to the manager at another branch and was told that they saw about 2600 customers per day, and that cashiers checkout 25-35 customers an hour1. For this reason I took $\mu$ to be 30 customers per hour.
The mathematics of the arrival process
I need to select an arrival rate function $\lambda(t)$. This function is used to specify the average rate at which people enter the store at time $t$. I’ll model the arrival process as a Poisson random measure, which is also known as a non-homogeneous Poisson process.
What this means is the following: if I let $X_n$ denote the arrival time of the $n$-th customer, then the sequence of customers $\lbrace X_n\rbrace$ forms a Poisson random measure if, amoung other things, the number of arrivals between times $t_0$ and $t_1$ is a Poisson random variable with mean
\[ \int_{t_0}^{t_1} \lambda(t) \, dt. \]
Note that $\lambda(t) \geq 0$. What this means is that we expect more people to arrive at the store when we look at longer time windows, and that we expect more arrivals during times when $\lambda(t)$ is large.
Next I need to actually specify an arrival rate function. My two constraints are that it needs to vary throughout the day, and that the average number of people in a day should be around 2700, i.e.
\begin{equation} \int_0^h \lambda(t) \, dt \approx 2700, \label{eq:constraint} \end{equation}
where $h$ specifies how many hours the store is open for in a day. The branch near me is open from 8am to 9pm, so $h = 13$. I decided to use the following rate function
\begin{equation} \lambda(t) = a + 2b \sin^2(\pi t/ h) = a+b - b\cos(2\pi t / h). \label{eq:rate function} \end{equation}
where $a$ and $b$ are choosen so that \eqref{eq:constraint} holds. Using \eqref{eq:rate function} and \eqref{eq:constraint} we have
\[ h(a+b) \approx 2700, \]
and in my simulations I vary $a$ and $b$ so that $h(a + b) = 2700$, while keeping $h$ at $13$. For the plots given above I set $a=158$ and $b=50$.
The mathematics of the checkout process
This process is much easier to model than the arrival process. My only requirement was that approximately 30 customers are checked out per hour, regardless of the time of day2. So I settled on modeling the amount of time at a checkout counter as an exponential random variable with rate 30.
Simulations
In the previous section, I defined the following variables:
- $\lambda(t)$ is the arrival rate function. It is the average number of people that enter the store at time $t$.
- $a$ and $b$ are parameters used to specify $\lambda(t)$. I looked at a bunch of these and choose the pair that looked most reasonable.
- $\mu$ is the service rate. It is the average number of customers that a cashier can checkout in an hour.
- $h$ is the number of hours the store is open for. In this case $h = 13$.
- $n_c$ is the number of counters at the store. I took $n_c$ to be $8$.
The simulations were run in Python using queueing-tool, the best queueing simulator known to mankind.
Modeling the Trader Joe’s checkout was straight forward, since all I needed was one queue for the checkout area. I created this with the following code:
import matplotlib.pyplot as plt
import queueing_tool as qt
import numpy as np
# Queueing parameters
a, b = 158, 50
h = 13.0
nc = 8
mu = 30.0
# Queueing process functions
rate = lambda t: a + b - b * np.cos(2 * np.pi * t / h)
arr = lambda t: qt.poisson_random_measure(t, rate, a + 2 * b)
ser = lambda t: t + np.random.exponential(1 / mu)
# The Queue
q = qt.QueueServer(nServers=nc, deactive_t=h,
arrival_f=arr, service_f=ser)For the traditional checkout, I needed a “Greedy Agent” type of customer that would always route themselves to the shortest line. Fortunately, this is already built into queueing-tool. The following code created the queueing network for shortest queue routing.
adjacency = {
0: {1: {'edge_type': 1}},
1: {k: {'edge_type': 2} for k in range(2, 2 + nc)}
}
qclass = {1: qt.QueueServer, 2: qt.QueueServer}
qargs = {1: {'nServers': 1,
'deactive_t': h,
'arrival_f': arr,
'service_f': lambda t: t,
'AgentClass': qt.GreedyAgent},
2: {'nServers': 1,
'service_f': ser}}
qn = qt.QueueNetwork(adjacency, q_classes=qclass, q_args=qargs)The full code for the simulation can be found in this gist. In case you’re interested, the network looks like so:
This above image was taken mid simulation; darker edges represent busier checkout lines.
Literature review
There is a ton of literature on queueing theory, but very little (to my knowledge) that gives good approximations to the waiting time distribution for the systems studied here. I can, however, point the interested reader to some papers on shortest queue length routing, and waiting time approximations in $M/G/m$ queues.
The optimality3 of shortest queue length routing for single-server queueing systems was first proved in [Winston, 1977] for Markovian systems, with extensions by [Weber, 1978]4 and [Ephremides et. al, 1980]. Unfortunately, shortest queue length routing is not always optimal as shown in [Whitt, 1986]5, but [Houck, 1986] showed via simulation that it is close to optimal in several systems. For slightly more complicated networks than the one presented here, Braess’s paradox can occur; see [Calvert et al., 1997]
As for the waiting times, there are several results for systems using shortest path routing. One can get bounds on the queue length distribution using techniques presented in [Halfin, 1985], [Lui et al., 1985], [Nelson et al., 1993], and [Lin et al., 1996] (using Little’s Law, this gives you the mean waiting time in steady state). Some of these results only evaluate long run performance, but they all fail to address systems with time varying arrival rates.
Approximations to the $M/G/m$ queue are studied by [Hokstad, 1978] and [Yao, 1985], and waiting time approximations studied by [Boxma et al., 1979]. The Pollaczek–Khinchine formula, which yields mean waiting time via Little’s Law. There is also Kingman’s formula for mean waiting time for a $G/G/1$ queue. I’m probably missing tons more, sorry.
-
Each of these branches had 9 registers. Also, during busy times they have baggers at half the checkout counters. ↩
-
This doesn’t mean that cashiers don’t get tired, just that when they are tired a new cashier takes their place or something. ↩
-
By optimal we mean it minimizes the expected value of the mean customer waiting time, maximizes the probability that no server is idle at time $t$, etc. ↩
-
He extended Winstons results to general service time distributions with non-decreasing failure rates. ↩
-
Whitt shows, via counter-examples, that shortest queue routing is not always optimal. He also looks at shortest expected delay routing (which is equivalent to shortest queue routing in Markovian systems) and shows that this routing discipline is not optimal for multi-server queues. ↩